3.3.- Hipótesis de los modelos

Los modelos de inventario que estudiamos a continuación se desarrollan bajo los siguientes supuestos:

1. El período de programación o gestión T representa la duración de cada ciclo de inventario. Se trata de una variable de decisión del sistema.

2. El inventario se repone al inicio de cada período de programación hasta el nivel de stock inicial S. Dicho nivel de stock, obtenido después de la reposición, es otra variable de decisión del sistema.

3. El inventario debe ser repuesto cuando el nivel de stock sea igual o inferior a s unidades (s representa el punto de pedido o de reposición). Cuando hay roturas, y si se admite la posibilidad de que la demanda pendiente sea totalmente atendida con la siguiente reposición, s puede ser una cantidad negativa y, en ese caso, -s representa el número de unidades de demanda a cubrir al final del ciclo de inventario.

4. El tamaño del lote Q representa el tamaño de la reposición. Si las roturas no están permitidas o cuando todas las roturas son pérdida de ventas, entonces Q = S. En el caso en que haya demanda diferida en el tiempo, esto es, cuando la rotura es recuperable y se satisface posteriormente, con la llegada de la siguiente reposición, ya que los clientes están dispuestos a esperar, Q es la suma del nivel inicial de stock (S) más el número total de pedidos pendientes en el ciclo de inventario (Q = S – s).

5. La tasa de reposición es infinita, es decir, la reposición es instantánea.

6. El tiempo de retardo es cero.

7. Se supone que el comportamiento del sistema durante el periodo T se repite sucesivamente a lo largo del tiempo.

8. El costo unitario de mantenimiento h es una constante, cuya dimensión es (dinero) / (cantidad) (tiempo).

9. El costo por pedido, que denotamos por A, es una constante, cuya dimensión es (dinero).

10. Cuando las roturas son completamente atendidas con la siguiente reposición, el costo unitario de rotura w 95 es constante y su dimensión es (dinero) / (cantidad) (tiempo).

11. Cuando las roturas se traducen en pérdida de ventas, el costo unitario de rotura  es una constante y su dimensión es (dinero) / (cantidad). En este caso, el costo de la rotura depende únicamente de la cantidad de roturas existente al final del período de programación y no de la duración de las mismas.

12. Sea d la demanda total durante el tiempo de programación T, y sea r la demanda promedio por período, es decir, r = d/T. La demanda promedio por periodo es determinista, pero la forma mediante la cual las cantidades de artículos son sacadas del inventario depende del momento en que éstos son retirados. Esa manera por la cual la demanda se distribuye durante el período de gestión será conocida como el patrón de demanda.

Este patrón de la demanda se conoce como “patrón de demanda potencial” (ver Naddor (1966), Datta y Pal (1988), Lee y Wu (2002)).

El gráfico 3.1 ilustra la cantidad de inventario durante el período de programación T para diferentes patrones de demanda potencial. T representa el periodo de programación, d es el tamaño de la demanda durante dicho periodo, S es el nivel inicial de stock y n es el patrón de demanda potencial. En todos los patrones hay S unidades en inventario al comienzo del período. Cuando n > 1, una porción mayor de la demanda se produce hacia el comienzo del período. Cuando n = 1, la demanda sigue un patrón uniforme, de forma que está repartida, de manera constante, a lo largo del período. Finalmente, cuando n < 1, se produce una parte mayor de la demanda al final del período.

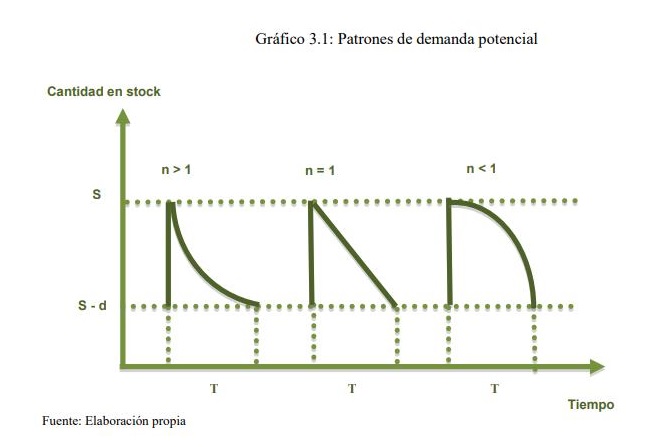
El nivel de inventario I(t) es una función decreciente, continua y diferenciable en el intervalo [0,T). Al comienzo del período de programación hay I(0) = S unidades en stock y, posteriormente, el nivel de stock se va reduciendo con el tiempo. Al final del período, el inventario es repuesto instantáneamente hasta el nivel S y, por tanto, comienza otra vez un nuevo ciclo de inventario.

En los apartados siguientes estudiaremos las políticas óptimas de inventario, tanto para el sistema en el cual no se admite la existencia de roturas, como para otros sistemas de inventario en los cuales las roturas están permitidas.