3.4.- Sistema de inventario con patrón de demanda potencial, sin roturas permitidas

Comenzamos analizando el sistema de inventario con patrón de demanda potencial cuando no se permiten roturas. En este caso, el nivel inicial de stock S al comienzo del ciclo de inventario T debe cubrir la demanda total d durante ese periodo T. Por lo tanto, S = d y la cantidad media I1(S) mantenida en inventario es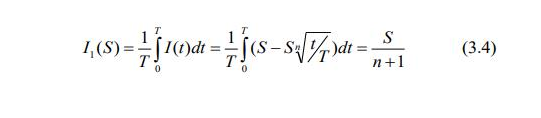

Por su parte, la rotura promedio en inventario I2(S) es igual a 0 porque no existen roturas. Además, como el nivel de stock inicial S debe ser igual a la demanda total d, y dicha demanda es igual a rT durante el período de programación, entonces tenemos que T = S/r. Así, el número de reposiciones por unidad de tiempo es R(S) = 1/T = r/S. El costo de mantenimiento por unidad de tiempo es C1(S) = hI1(S), el costo de rotura es cero y el costo de reposición por unidad de tiempo es C3(S) = AR(S) = Ar/S. Así, el costo total C(S) por unidad de tiempo es la suma de estos costos y viene dado por la expresión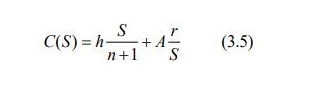

En el caso particular de que n = 1 (patrón de demanda uniforme), la política ya mencionada coincide con la clásica cantidad económica de pedido (EOQ). Además, cuando el índice n del patrón de la demanda es mayor que 1, el costo mínimo de la política óptima es siempre menor que el costo (2hAr)1/2 de la política EOQ. Sin embargo, si n < 1, entonces el costo mínimo de la política óptima es mayor que el costo de la política EOQ, ya que la demanda se concentra más al final del periodo y hay mayor coste de mantenimiento.